In this article, we will discuss how to do a two sample t-test in R with some practical examples.
What is Two-sample t-test for mean?
Two sample t-test is used to determine whether there is a significant difference between the two population means given for the two samples with unknown population variance.
Conditions required to conduct two sample t-test for mean
Assumptions for Two Sample Mean t-test
- Both Population variances are unknown.
- Both sample size should be small.
- Both samples should be drawn at random from their respective populations.
- Two Samples should be independent of each other.
- Both Populations should follow a normal distribution.
Hypothesis for the two sample t-test for mean
Let x̅1 denote the sample mean for a random sample from population 1.
x̅2 denote the sample mean for a random sample from population 2.
µ1 denotes the mean for population 1
µ2 denotes the mean for population 2
Null Hypothesis:
H0 : µ1 = µ2 Both population means are equal.
Alternative Hypothesis: Three forms of alternative hypothesis are as follows:
- Ha : µ1 – µ2 <0 The difference between two population means is less than 0 i.e.mean for population 1 is less than the mean for population 2.It is called lower tail test (left-tailed test).
- Ha : µ1 – µ2 >0 The difference between two population means is greater than 0 i.e. mean for population 1 is greater than the mean for population 2. It is called Upper tail test (right-tailed test).
- Ha : µ1 – µ2 ≠ 0 The difference between two population means is not equal to 0 i.e. mean for population 1 is not equal to mean for population 2. It is called two tail test.
Formula for the test statistic two sample t test is:
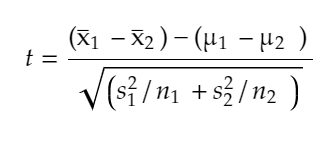
where :
x̅1 : sample mean for population 1
x̅2: sample mean for population 2
µ1 : mean for population 1
µ2 : mean for population 2
n1 : sample size for sample mean from population 1.
n2 : sample size for sample mean from population 2.
s21 : variance for sample 1
s22 : variance for sample 2
df : degree of freedom
when variance are unequal and unknown then df will be:
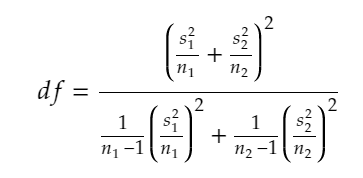
Function in R for t-test
To perform two sample t-test for the mean we will use the t.test() function in R from the stats library.
The t.test() function uses the following basic syntax:
t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95, ...)
where :
x,y: It tells us about the datasets used in the test.
alternative: The alternative hypothesis for the test.
mu: The true value of the mean.
paired: Specify it is a paired t-test or not.
var. equal: a logical variable indicates whether to treat the two variances as being equal.
conf. level: confidence level of the interval
Summary for the two sample t-test for mean
| Left-tailed Test | Right-tailed Test | Two-tailed Test | |
| Null Hypothesis | H0 : µ1 – µ2 ≥0 | H0 : µ1 – µ2 ≤0 | H0 : µ1 – µ2 =0 |
| Alternate Hypothesis | Ha : µ1 – µ2 <0 | Ha : µ1 – µ2 >0 | Ha : µ1 – µ2 ≠ 0 |
| Test Statistic | t = ( x̅1 – x̅2 ) – (µ1 – µ2) / √(σ21/n1 + σ22 /n2) | t = ( x̅1 – x̅2 ) – (µ1 – µ2) / √(σ21/n1 + σ22 /n2) | t = ( x̅1 – x̅2 ) – (µ1 – µ2) / √(σ21/n1 + σ22 /n2) |
| Decision Rule: p-value approach (where α is level of significance) | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 |
| Decision Rule: Critical-value approach | If t ≤ -tα then Reject H0 | If t ≥ tα then Reject H0 | If t ≤ -tα/2 or t ≥ tα/2 then Reject H0 |
How to do two sample t-test for mean in R?
We will calculate the test statistic by using a two sample t-test for the mean.
Procedure for Two Sample t-test for mean
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
Step 2: Decide the level of significance α (alpha).
Step 3: Calculate the test statistic using the t.test() function from R.
Step 4: Interpret the two sample t-test results.
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Let’s see practical examples that show how to use the t.test() function in R.
Example for Two Sample t-test
Example 1: Two-tailed test in R with unknown equal variance.
Body weight among boys and girls in class are known to be normally distributed, each with sample standard deviations for girls is 25 and for boys is 23.
A teacher wants to know if the mean body weight between girls and boys in class are different, so she selects two random samples of boys and girls each of size 20 from the class and records their weights.
Wants to determine if the mean weight is different between boys and girls with 5% level of significance.
Solution : Given data:
sample size for boys (n1) = 20
sample size for girls (n2) = 20
sample standard deviation for boys (σ1) = 23
sample standard deviation for girls (σ2) = 25
Now we will solve this example with the step-by-step procedure.
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
µ1 denotes the mean for boys
µ2 denotes the mean for girls
Null Hypothesis: The body weight for girls and boys are equal.
H0 : µ1 = µ2
Alternate Hypothesis : The body weight for girls and boys are not equal.
Ha : µ1 ≠ µ2
Step 2: level of significance (α) = 0.05
Step 3: Calculate the test statistic using a t.test() function in R using the below code.
# Define the datasets for boys and girls boys_dataset = c(56,65,47,46,60,56,45,39,50,45,39,42,42,33,47,57,45,50,45,42) summary(boys_dataset) girls_dataset = c(56,65,37,47,60,46,35,41,40,45,34,42,42,43,37,47,45,50,45,42) # Perform the two sample t-test t.test(x=boys_dataset, y=girls_dataset, mu=0,var.equal = FALSE,paired = FALSE,alternative = "two.sided")
Specify the alternative hypothesis as “two.sided” because we are performing a two-tailed test. The results are as follows.
Welch Two Sample t-test
data: boys_dataset and girls_dataset
t = 1.0381, df = 37.998, p-value =
0.3058
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.470469 7.670469
sample estimates:
mean of x mean of y
47.55 44.95
Step 4: Interpret the two sample test results.
How to interpret two sample z-test results in R?
Let’s see the interpretation of z-test results in R.
data: This gives information about the data set used in the one-sample t-test. In this, we use dataset vector as data.
t: It is the test statistic of the t-test. In our case test statistic = -1.5119
df: It is the degree of freedom for the t-test statistic. In our case df=5
p-value: This is the p-value corresponding to t-test statistic i.e. -1.5119 and degree of freedom i.e. 5. In our case, the p-value is 0.09549.
alternative: It is the alternative hypothesis used for the t-test. In our case, an alternative hypothesis is true to mean is less than 553 i.e left tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true mean. Here the 95% confidence interval is [-∞,553.8875].
sample estimates: It gives the sample mean. In our case sample mean is 550.33
Step 6: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[ 0.09549] is not less than the level of significance (α) = 0.05, we fail to reject the null hypothesis.
This means we do not have sufficient evidence to say that the mean weight of the almonds in the dry fruits is different from 553 grams.
data: This gives information about the vector used in the z-test. x represents the data set for boys and y represents the data set for girls.
z: It is the test statistic of the z-test. In our case, test statistic = -0.68424.
p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.4938.
alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis the IQ level for girls and boys are not equal, i.e. two-tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true mean. Here the 95% confidence interval is [-14.781532,7.131532].
sample estimates: It gives the sample means.In our case, the sample mean for boys=106.350 and sample mean for girls =110.175.
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[ 0.4938] is greater than the level of significance (α) = 0.05, we fail to reject the null hypothesis.
This means we have sufficient evidence to say that IQ level for boys and girls are equal in 10th class.
Example 2: Left-tailed two sample test in R with known unequal variance.
The two independent populations taken from two shops in a small town.The first shop A sells “traditional” lime juice. However the second shop B is selling “Special” Mojito. We selects the two random sample of sales for each drink(shop) and records their sales for 35 days to determine if sales for “Special” Mojito out performed sales of “traditional” lime juice at 5% level of significance. The population variances for lime juice sales is 15 and for Mojito is 12.
Solution : Given data:
sample size for lime juice sales (n1) = 35
sample size for Mojito sales (n2) = 35
Population standard deviation for lime juice sales (σ1) = 15
Population standard deviation for Mojito sales (σ2) = 12
Lets perform z-test in this example with the step-by-step procedure.
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
µ1 denotes the mean for lime juice sales
µ2 denotes the mean for Mojito sales
Null Hypothesis: The sales for lime juice sales and Mojito sales are equal.
H0 : µ1 = µ2
Alternate Hypothesis : The sales for Mojito sales are greater and sales for lime juice.
Ha : µ1 – µ2 <0 i.e µ2 > µ1
Step 2: level of significance (α) = 0.05
Step 3: Calculate the test statistic using a z.test() function in R using the below code.# Define the datasets for both drinkslime_juice_sales = c(56,65,37,47,66,76,75,31,80,45,34,42,42,23,67,47,45,50,45,42,59,34,50,48,65,41,53,41,36,39,51,69,30,52,42)mojito_sales = c(51,47,53,40,70,49,63,71,47,62,65,62,56,74,49,33,80,60,46,65,48,61,54,67,65,48,46,66,52,65,62,59,63,44,50)# Perform the two sample z-testz.test(x=lime_juice_sales, y=mojito_sales, mu=0, sigma.x=15, sigma.y=12,alternative = “less”)
Specify the alternative hypothesis as “less” because we are performing a left-tailed test. The results are as follows.#ResultsTwo-sample z-Testdata: lime_juice_sales and mojito_salesz = -2.3582, p-value = 0.009181alternative hypothesis: true difference in means is less than 095 percent confidence interval: NA -2.316342sample estimates:mean of x mean of y 49.28571 56.94286
Step 4: Interpret the two sample test results.
How to interpret two sample z-test results in R?
Let’s see the interpretation of z-test results in R.
data: This gives information about the vector used in the z-test. x represents the data set for lime juice sales and y represents the data set for mojito sales.
z: It is the test statistic of the z-test. In our case, test statistic = -2.3582.
p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.009181.
alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis the sales for Mojito sales are greater and sales for lime juice , i.e. left-tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true mean.
sample estimates: It gives the sample means.In our case, the sample mean for lime juice sales = 49.28571and sample mean for mojito sales = 56.94286
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[ 0.009181] is less than the level of significance (α) = 0.05, we reject the null hypothesis.
This means we have sufficient evidence to say that the sales for mojito drink is out performed as comapre to lime juice sales in the town.
A statistician claims that the average score on logical reasoning test taken by students who major in Physics is less than that of students who major in English. The result of the exams, given to 22 Physics students and 33 English students, is shown here. Is there enough evidence to reject the statistician’s claim at α=0.05α=0.05? Assume that the standard deviations for the two populations are not equal.
The two sample t-test is used to determine whether the two populations are equal or not then population variance is unknown.
Summary
I hope you found the above article on two sample t-test in R with Examples informative and educational.