In this article, we will discuss how to do a one-sample t-test in R with some practical examples.
What is One-sample t-test for mean?
The one-sample t-test for the mean is used to test whether the population mean is equal to the pre-defined (standard/hypothetical) mean (μ) value when the population standard deviation is unknown and sample size is small.
What are the conditions required for conducting a one-sample t-test for mean?
Assumptions for One Sample Mean t-test
- The parent population from which the sample is drawn should be normal.
- The sample observations should be independent of each other i.e sample should be random.
- The population standard deviation is unknown.
Hypothesis for the one sample t-test for mean
Let μ0 denote the hypothesized value for the mean and x̄ denotes the sample mean.
Null Hypothesis:
H0 : x̄= μ0 The population means is equal to hypothesized(standard) mean.
Alternative Hypothesis: Three forms of alternative hypothesis are as follows:
- Ha : x̄< μ0 Population mean is less than the hypothesized mean.It is called lower tail test (left-tailed test).
- Ha : x̄>μ0 Population mean is greater than the hypothesized mean.It is called Upper tail test(right-tailed test).
- Ha : x̄ ≠μ0 Population mean is not equal to hypothesized mean.It is called two tail test.
Formula for the test statistic of one sample t- test for mean is:
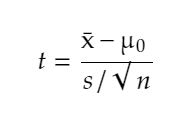
where :
x̄: observed sample mean
μ0: hypothesized population mean
n: sample size
s: sample standard deviation with n-1 degree of freedom
Function in R for t-test
t.test() function in R from the stats package is used to perform a one-sample t-test for mean.
Syntax:-
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, ...)
where :
x,y: given sample data. y will be none if only one sample is given.
alternative: The alternative hypothesis for the t-test.
mu: The true value of the mean.
paired: Specify it is a paired t-test or not.
var. equal: a logical variable indicates whether to treat the two variances as being equal.
conf. level: confidence level of the interval
Summary for the one sample t-test for mean
| Left-tailed Test | Right-tailed Test | Two-tailed Test | |
| Null Hypothesis | H0 : x̄≥ μ0 | H0 : x̄≤ μ0 | H0 : x̄= μ0 |
| Alternate Hypothesis | Ha : x̄< μ0 | Ha : x̄> μ0 | Ha : x̄ ≠ μ0 |
| Test Statistic | t= (x̄ – μ0 )/(s/ √ n) | t= (x̄ – μ0 )/(s/ √ n) | t= (x̄ – μ0 )/(s/ √ n) |
| Decision Rule: p-value approach (where α is level of significance) | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 |
| Decision Rule: Critical-value approach | If t ≤ -tα then Reject H0 | If t ≥ tα then Reject H0 | If t ≤ -tα or t ≥ tα then Reject H0 |
How to do one sample t-test for mean in R?
We will calculate the test statistic with one-sample t-test for the mean.
Procedure to perform One Sample t-test for mean.
Step 1: Define the both Null Hypothesis and Alternate Hypothesis.
Step 2: Decide the level of significance α (i.e. alpha).
Step 3: Check the assumptions for the one-sample t-test for the mean using the below function.
qqnorm(dataset) qqline(dataset)
Step 4: Calculate the test statistic using the t.test() function from R.
Step 5: Interpret the t-test results.
Step 6: Determine the rejection criteria for the given confidence level and interpret the results whether the test statistic lies in the rejection region or non-rejection region.
Let’s see practical examples that show how to use the t.test() function in R.
Example of One Sample t-test in R
The Food Company claims that its dry fruit boxes contain, on average, 553 grams of almonds. We suspect that the dry fruit boxes contain, on average, less than claimed. You decided to test the claim by inspecting 6 randomly selected boxes, and get the following weights:
544, 551, 548, 556, 549, 554.
Assume that the amount of almonds in a box follows a normal distribution. Test at 5% level of significance.
Solution: Given data :
sample size (n) = 6
hypothesized mean value (μ0)= 553
level of significance (α) = 0.05
confidence level = 0.95
Let’s solve this example by the step-by-step procedure.
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
let μ be the mean weight of almonds
Null Hypothesis: the mean weight of almonds in the boxes is equal to 553 grams
H0 : μ = 553
Alternate Hypothesis: the mean weight of almonds in the boxes is less than 553 grams
Ha : μ < 553
Step 2: level of significance (α) = 0.05
Step 3: Lets check the assumptions.
# Define given dataset dataset <- c(546, 551, 548, 556, 549, 554) #Create qqplot for the dataset qqnorm(dataset) qqline(dataset)
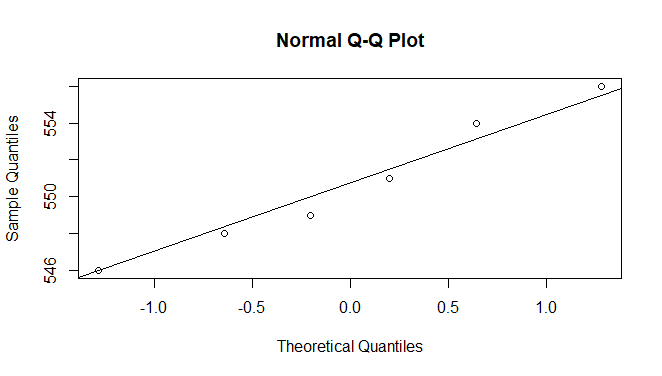
Since the data lies close to the line y=x and has no big deviations from the line, it’s fine to consider the sample as coming from a normal distribution. We can proceed further with our hypothesis test.
Step 4: Calculate the test statistic using the t.test() function from R.
# Define given dataset dataset <- c(546, 551, 548, 556, 549, 554) #Create qqplot for the dataset qqnorm(dataset) qqline(dataset) # Perform one-sample t-test t.test( x= data,mu=553, alternative = "less",conf.level = 0.95)
Specify the alternative hypothesis as “less” because we are performing left tailed test. The results for the one-sample t-test are as follows.
#Results
One Sample t-test
data: dataset
t = -1.5119, df = 5, p-value = 0.09549
alternative hypothesis: true mean is less than 553
95 percent confidence interval:
-Inf 553.8875
sample estimates:
mean of x
550.3333
Step 5: Interpret the t-test results.
How to interpret t-test results in R?
Let’s see the interpretation of t-test results in R.
data: This gives information about the data set used in the one-sample t-test. In this, we use dataset vector as data.
t: It is the test statistic of the t-test. In our case test statistic = -1.5119
df: It is the degree of freedom for the t-test statistic. In our case df=5
p-value: This is the p-value corresponding to t-test statistic i.e. -1.5119 and degree of freedom i.e. 5. In our case, the p-value is 0.09549.
alternative: It is the alternative hypothesis used for the t-test. In our case, an alternative hypothesis is true to mean is less than 553 i.e left tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true mean. Here the 95% confidence interval is [-∞,553.8875].
sample estimates: It gives the sample mean. In our case sample mean is 550.33
Step 6: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[ 0.09549] is not less than the level of significance (α) = 0.05, we fail to reject the null hypothesis.
This means we do not have sufficient evidence to say that the mean weight of the almonds in the dry fruits is different from 553 grams.
What package is needed for t-test in R?
The R Stats Package is needed to do a t-test in R.