In this article, we will discuss how to do a two-proportion z-test in R with some practical examples.
What is Two Proportion z-test ?
The Two Proportion Z-test is used to conduct a hypothesis test about the difference between the proportions of two populations.
Conditions required to conduct two proportion z test
Assumptions for the two proportion z-test are as follows:-
- Both samples should be drawn at random from their respective population.
- Populations should follows a binomial distribution.
- n1p1>10 ,n1(1-p1)>10 & n2p2>10 ,n2(1-p2) >10 where n1,n2 are sample size and p1 & p2 are sample proportions for two populations.
- Both populations size should be 10 times larger than the sample size.
Hypothesis for the two proportion z-test
Let p1 denote the sample proportion for a simple random sample from population 1.
p2 denotes the sample proportion for a simple random sample from population 2.
P1 denotes the proportion for population 1
P2 denotes the proportion for population 2
Null Hypothesis:
H0 : P1= P2 Both population proportions are equal.
Alternative Hypothesis: Three forms of alternative hypothesis are as follows:
- Ha : P1-P2 <0 The difference between two population proportions is less than 0 i.e.proportion for population 1 is less than the proportion for population 2.It is called lower tail test (left-tailed test).
- Ha : P1-P2 >0 The difference between two population proportions is greater than 0 i.e.proportion for population 1 is greater than the proportion for population 2.It is called Upper tail test (right-tailed test).
- Ha : p1-p2 ≠ 0 The difference between two population proportions is not equal to 0 i.e.proportion for population 1 is not equal to proportion for population 2.It is called two tail test.
Formula for the test statistic two proportion Z test is:
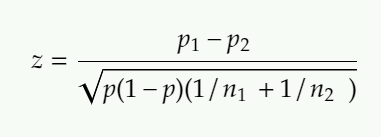
where :
n1 : sample size for sample proportion from population 1.
n2 : sample size for sample proportion from population 2.
p1 : sample proportion for population 1
p2 : sample proportion for population 2
p : pooled sample proportion
where
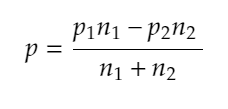
Functions in R for two proportion z-test
To perform two proportion z-test, we will use the prop.test() functions from the R stats library.
The prop.test() function uses the following basic syntax:
prop.test(x, n, p = NULL, alternative = c("two.sided", "less", "greater"),
conf.level = 0.95, correct = TRUE)
where:
x : Vector of number of successes
n: Vector of a number of trials.
p: The vector of probabilities of success.
alternative: The alternative hypothesis for the test. It can be ‘greater’, ‘less’, ‘two.sided’ based on the alternative hypothesis.
conf. level: confidence level of the interval
correct: a logical indicating whether Yates’ continuity correction should be applied or not where it is possible
Summary for the Two Proportion Z-test
| Left-tailed Test | Right-tailed Test | Two-tailed Test | |
| Null Hypothesis | H0 : P1-P2 ≥0 | H0 : P1-P2 ≤0 | H0 : P1-P2 =0 |
| Alternate Hypothesis | Ha : P1-P2 <0 | Ha : P1-P2 >0 | Ha : P1-P2 ≠ 0 |
| Test Statistic | z = (p1– p2)/√(p(1- p)/(1/n1 + 1/n2) | z = (p1– p2)/√(p(1- p)/(1/n1 + 1/n2) | z = (p1– p2)/√(p(1- p)/(1/n1 + 1/n2) |
| Decision Rule: p-value approach (where α is level of significance) | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 | If p-value ≤α then Reject H0 |
| Decision Rule: Critical-value approach | If z ≤ -zα then Reject H0 | If z ≥ -zα then Reject H0 | If z ≤ -zα/2 or z ≥ zα/2 then Reject H0 |
How to do two proportion z-test in R?
We will calculate the test statistic by using two proportion z-test.
Procedure to perform Two Proportion Z-Test in R
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
Step 2: Decide the level of significance α (alpha).
Step 3: Calculate the test statistic using the prop.test() function from R.
Step 4: Interpret the two-proportion z-test results.
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Let’s see practical examples that show how to use the prop.test() function in R.
Examples of Two Proportion z-test in R
Example 1: Two-tailed two proportion test in R
In a large city, X, 189 from a sample of 900 students had a defective eye-sight. In the other large city Y,192 from a sample of 1200 students had the same eye defect. We want to study whether there is any significant difference between the two proportions at the 5% level of significance.
Solution: Given data :
sample size for City X (n1) = 900
sample size for City Y (n2) = 1200
sample proportion for City X (p1) = 189/900 = 0.21
sample proportion for City Y (p2) = 192/1200 = 0.16
Let’s solve this example by the step-by-step procedure.
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
let P1 be the population proportion for City X.
P2 be the population proportion for City Y.
Null Hypothesis: Both population proportions are equal.
H0 : P1 = P2
Alternate Hypothesis: Both population proportions are not equal.
Ha: P1 ≠ P2
Step 2: level of significance (α) = 0.05
Step 3: Calculate the test statistic using a prop.test() function in R using the below code.
# Perform two-proportion z-test prop.test(x = c(189, 192), n = c(900, 1200),alternative = "two.sided")
Specify the alternative hypothesis as “two.sided” because we are performing a two-tailed test. The results for the two-proportion z-test are as follows.
#Results 2-sample test for equality of proportions with continuity correction data: c(189, 192) out of c(900, 1200) X-squared = 8.3239, df = 1, p-value = 0.003913 alternative hypothesis: two.sided 95 percent confidence interval: 0.0152883 0.0847117 sample estimates: prop 1 prop 2 0.21 0.16
Step 4: Interpret the two-proportion test results.
How to interpret two-proportion z-test results in R?
Let’s see the interpretation of two-proportion z-test results in R.
data: This gives information about the vector used in the two-proportion z-test.
X-squared: the value of Pearson’s chi-squared test statistic.
df: the degree of freedom of the approximate chi-squared distribution of the test statistic.
p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.003913.
alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis is population proportions are not equal, i.e. two-tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true proportion. Here the 95% confidence interval is [0.0152883,0.0847117].
sample estimates: It gives the sample proportions. In our case, prop 1 = 0.21 and prop 2 = 0.16.
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[0.003913] is less than the level of significance (α) = 0.05, we reject the null hypothesis.
This means we have sufficient evidence to say that the population proportions are not equal.
Example 2: Right-tailed two proportion test in R
Before an increase in excise duty on coffee,800 persons out of a sample of 1000 persons were found to be coffee drinkers. After an increase in excise duty, 900 people were coffee drinkers in a sample of 1200 people. We want to study whether there is a significant decrease in the consumption of coffee after the increase in excise duty at the 5% level of significance.
Solution: Given data :
sample size before excise duty(n1) = 1000
sample size after excise duty = 1200
sample proportion before excise duty (p1) = 800/1000 = 0.80
sample proportion after excise duty (p2) = 900/1200 = 0.75
Let’s solve this example by the step-by-step procedure.
Step 1: Define the Null Hypothesis and Alternate Hypothesis.
let P1 be the population proportion for Coffee drinkers before excise duty.
P2 be the population proportion for Coffee drinkers after excise duty.
Null Hypothesis: Both population proportions for Coffee drinkers are equal.
H0 : P1 = P2
Alternate Hypothesis: Population proportions for Coffee drinkers after excise duty is less than the Population proportions for Coffee drinkers before excise duty.
Ha: P1 > P2
Step 2: level of significance (α) = 0.05
Step 3: Calculate the test statistic using prop.test() function in R using the below code.
# Perform two-proportion z-test prop.test(x = c(800,900), n = c(1000, 1200),alternative = "greater")
Specify the alternative hypothesis as “greater” because we are performing a right-tailed test. The results for the two-proportion z-test are as follows.
#Results 2-sample test for equality of proportions with continuity correction data: c(800, 900) out of c(1000, 1200) X-squared = 7.4826, df = 1, p-value =0.003115 alternative hypothesis: greater 95 percent confidence interval: 0.01983221 1.00000000 sample estimates: prop 1 prop 2 0.80 0.75
Step 4: Interpret the two-proportion test results.
How to interpret two-proportion z-test results in R?
Let’s see the interpretation of two-proportion z-test results in R.
data: This gives information about the vector used in the two-proportion z-test.
X-squared: the value of Pearson’s chi-squared test statistic.
df: the degree of freedom of the approximate chi-squared distribution of the test statistic.
p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.003115.
alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis is population proportions for Coffee drinkers after excise duty is less than the Population proportions for Coffee drinkers before excise duty, i.e. right-tailed.
95 percent confidence interval: This gives us a 95% confidence interval for the true proportion. Here the 95% confidence interval is [0.01983221,1.00000000].
sample estimates: It gives the sample proportions. In our case, prop 1 = 0.80 and prop 2 = 0.75.
Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.
Conclusion:
Since the p-value[0.003115] is less than the level of significance (α) = 0.05, we reject the null hypothesis.
This means we have sufficient evidence to say that the population proportions for coffee drinkers decrease after excise duty.
Two Proportion z-test FAQ
The R Stats Package is needed to do a t-test in R.
Summary
I hope you found the above article on How to Perform a Two Proportion z-test in R with Examples informative and educational.