Paired t-test in R with Examples

In this article, we will discuss how to do a paired t-test in R with some practical examples.

What is paired t-test ?

Paired test is used when we have the two related samples. Paired test is used to check whether there is a significant difference between two population means when their data is in the form of matched pairs.

Conditions required to conduct paired t-test

Assumptions for Paired t-test are as follows:

• The parent population from which the sample is drawn should be normal.
• The samples should be independent of each other.
• The sample size should be equal for both the samples, i.e. n₁ = n₂.
• The dependent variable should be continuos.

Hypothesis for the paired t-test

Let μ_d denote the mean difference.

Null Hypothesis:

H₀ : μ_d = 0  There is no difference between the two means.

Alternative Hypothesis: Three forms of alternative hypothesis are as follows:

• H_a :  μ_d < 0  The mean difference is less than zero. It is lower tail test (left-tailed test).
• H_a : μ_d > 0 The mean difference is greater than zero. It is Upper tail test(right-tailed test).
• H_a : μ_d ≠ 0 The mean difference is not equal to zero. It is called a two-tailed test.

Formula for the test statistic of the paired t-test is:

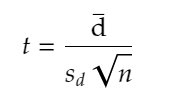
where:

d̅: mean of the difference between two given sample means

n: sample size.

s_d : standard deviation of d.

Function in R for Paired t-test

To perform paired t-test for the mean we will use the t.test() function in R from the stats library.

The t.test() function uses the following basic syntax:

t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"),
 mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95, ...)

where :

x,y: x and y represent the two samples datasets.

alternative: The alternative hypothesis for the test.

mu: The true value of the mean.

paired: Specify it is a paired t-test or not. Here we will write True.

var. equal: a logical variable indicates whether to treat the two variances as being equal.

conf. level: confidence level of the interval

Summary for the paired t-test for mean

	Left-tailed Test	Right-tailed Test	Two-tailed Test
Null Hypothesis	H0 : μd ≥ 0	H0 : μd ≤ 0	H0 : μd = 0
Alternate Hypothesis	Ha : μd < 0	Ha : μd > 0	Ha : μd ≠ 0
Test Statistic	t= d̅ /(sd√ n)	t= d̅ /(sd√ n)	t= d̅ /(sd√ n)
Decision Rule: p-value approach (where α is level of significance)	If p-value ≤α then Reject H0	If p-value ≤α then Reject H0	If p-value ≤α then Reject H0
Decision Rule: Critical-value approach	If t ≤ -tα then Reject H0	If t ≥ tα then Reject H0	If t ≤ -tα/2 or t ≥ tα/2 then Reject H0

How to do paired t-test in R?

We will calculate the test statistic by using a paired t-test.

Procedure to perform paired t-test.

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

Step 2: Decide the level of significance α (alpha).

Step 3: Calculate the test statistic using the t.test() function from R.

Step 4: Interpret the paired t-test results.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Let’s see practical examples that show how to use the t.test() function in R.

Examples of Paired t-test in R

Example 1: Right-tailed paired t-test in R

A training program was conducted to improve participant’s knowledge of the R language. Data of Test Results were collected from a selected sample both before and after the R training program. Test the hypothesis that the training is effective to improve participants’ knowledge of R language at a 5% level of significance.

Solution: Given data

before data : 39,43,41,32,37,40,42,40,37,38
after data : 42,45,42,43,40,44,40,43,41,40

Let’s solve this example by the step-by-step procedure.

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

let μ₁  be the population mean for the data before the training.

μ₂  be the population mean for the data after the training.

μ_d = μ₂ – μ₁

Null Hypothesis: Both population means are equal.

H₀ : μ_d = 0 i.e. μ₁ = μ₂

Alternate Hypothesis: Population mean after the training is greater than the population mean before the training.

H_a:  μ_d > 0 i.e. μ₂ > μ₁ (right-tailed test)

Step 2: level of significance (α) = 0.05

Step 3: Calculate the test statistic using the t.test() function in R using the below code.

# Define the datasets

before <- c(39,43,41,32,37,40,42,40,37,38)
after <- c(42,45,42,43,40,44,40,43,41,40)

# Perform the paired  t-test

t.test(x=before,y=after,paired = TRUE,alternative = "greater")

Specify the alternative hypothesis as “greater” because we are performing a right-tailed test. The results are as follows.

#Results

Paired t-test

data:  before and after
t = -2.9876, df = 9, p-value = 0.9924
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 -5.002085       Inf
sample estimates:
mean of the differences 
                   -3.1 

Step 4: Interpret the paired test results.

How to interpret the paired t-test results in R?

Let’s see the interpretation of the paired t-test results in R.

data: This gives information about the vector used in the paired t-test. x represents the data set before the training and y represents the data set after the training.

t: It is the test statistic of the t-test. In our case test statistic = -2.9876

df: It is the degree of freedom for the t-test statistic. In our case df=9

p-value: This is the p-value corresponding to t-test statistic i.e. – 2.9876 and degree of freedom i.e. 9. In our case, the p-value is 0.9924.

alternative: It is the alternative hypothesis used for the t-test. In our case, an alternative hypothesis is a population mean after the training is greater than the population mean before the training. i.e right tailed.

95 percent confidence interval: This gives us a 95% confidence interval for the true mean. Here the 95% confidence interval is [-5.002085,∞].

sample estimates: It gives the mean of the difference. In our case sample mean of the difference is -3.1.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Conclusion:

Since the p-value[ 0.9924] is not less than the level of significance (α) = 0.05, we fail to reject the null hypothesis.

This means we do not have sufficient evidence to say that the training is effective for the students.

Example 2: Left-tailed paired t-test in R

For instance, let’s say that we work at a large drug company, and we are testing a new drug A, which helps to reduce diabetes. We find 1000 individuals with high diabetes of average 140 mg/dL blood sugar level with a standard deviation of 10 mg/dL, and we provide them the drug A for a month, and then measure their blood sugar level again. We find that the mean blood sugar level has decreased to 130 mg/dL with a standard deviation of 8 mg/dL.

Solution:

Let’s solve this example by the step-by-step procedure.

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

let μ₁  be the population mean of blood sugar level before taking the drug A.

μ₂  be the population mean of blood sugar level after taking the drug A .

μ_d = μ₂ – μ₁

Null Hypothesis: Both population means are equal.

H₀ : μ_d = 0 i.e. μ₁ = μ₂

Alternate Hypothesis: Population mean after taking the drug A is less than the population mean before taking the drug A.

H_a:  μ_d < 0 i.e. μ₂ < μ₁ (left-tailed test)

Step 2: level of significance (α) = 0.05

Step 3: Calculate the test statistic using the t.test() function in R using the below code.

# Using seed function to generate the same random number every time with the given seed value
set.seed(1000)

#create a the pre dataset with 1000 values
pre_Treatment <- c(rnorm(1000, mean = 140, sd = 10))
#create a the post dataset with 1000 values
post_Treatment <- c(rnorm(1000, mean = 130, sd = 8))

# Perform the paired  t-test

t.test(pre_Treatment, post_Treatment, paired = TRUE,alternative = "less")

Specify the alternative hypothesis as “less” because we are performing a left-tailed test. The results are as follows.

#Results

Paired t-test

data:  pre_Treatment and post_Treatment
t = 25.432, df = 999, p-value = 1
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
     -Inf 10.50804
sample estimates:
mean of the differences 
               9.869133 

Step 4: Interpret the paired test results.

How to interpret the paired t-test results in R?

Let’s see the interpretation of the paired t-test results in R.

data: This gives information about the vector used in the paired t-test. x represents the data set before the training and y represents the data set after the training.

t: It is the test statistic of the t-test. In our case test statistic = 25.432

df: It is the degree of freedom for the t-test statistic. In our case, df=999

p-value: This is the p-value corresponding to t-test statistic i.e. 25.432 and degree of freedom i.e. 999. In our case, the p-value is 1.

alternative: It is the alternative hypothesis used for the t-test. In our case, an alternative hypothesis is a population mean after taking the drug A is less than the population mean before taking the drug A. i.e left tailed.

95 percent confidence interval: This gives us a 95% confidence interval for the true mean. Here the 95% confidence interval is [-∞,10.50804].

sample estimates: It gives the mean of the difference. In our case, the sample mean of the difference is 9.869133.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Conclusion:

Since the p-value[1] is greater than the level of significance (α) = 0.05, we fail to reject the null hypothesis.

This means we do not have sufficient evidence to say that drug A is effective for the patients.

Paired t-test FAQ

Summary

I hope you found the above article on Paired t-test in R with Examples informative and educational.