One Sample Proportion z-test in R with Examples

In this article, we will discuss how to do a one- sample proportion z-test in R with some practical examples.

What is One- Sample Proportion z-test ?

One-sample proportion z-test is used to conduct a hypothesis test about a population proportion(p). It is used to estimate the difference between the proportion of responses(or a number of successes) in a sample data and the actual proportion in the population data from which we draw the sample.

Conditions required to conduct one sample proportion z test

Assumptions for the one sampleproportion z-test are as follows:-

• The sample should be drawn at random from the population.
• Population should follow a binomial distribution.
• np₀>10 & n(1-p₀)>10 where n is sample size and p is the hypothesized value for the population proportion.
• The population size should be 10 times larger than the sample size.

Hypothesis for the one sample proportion z-test

Let p₀ denote the hypothesized value for the proportion.

p denotes the population proportion

Null Hypothesis:

H₀ : p=p₀ The population proportion is equal to hypothesized proportion.

Alternative Hypothesis: Three forms of alternative hypothesis are as follows:

• H_a : p < p₀ Population proportion is less than the hypothesized proportion.It is called lower tail test (left-tailed test).
• H_a : p > p₀ Population proportion is greater than the hypothesized proportion.It is called Upper tail test(right-tailed test).
• H_a : p ≠ p₀ Population proportion is not equal to hypothesized proportion.It is called two tail test.

Formula for the test statistic one proportion Z test is:

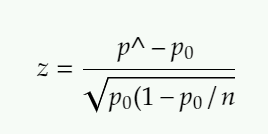
where :

n: sample size

p^{^}: observed sample proportion

p₀: hypothesized population proportion

Functions in R for one proportion z-test

To perform one proportion z-test, we will use the following functions from the R stats library.

We will use binom.test() or prop.test() function from R stats library

binom.test() :

If n ≤ 30 i.e when sample size is small then we use binom.test() function to perform one -proportion z-test.

The binom.test() function uses the following basic syntax:

binom.test(x, n, p = 0.5,
           alternative = c("two.sided", "less", "greater"),
           conf.level = 0.95)

where:

x: The number of successes

n: The number of trials.

p: The hypothesized probability of success.

alternative: The alternative hypothesis for the test.It can be ‘greater’, ‘less’, ‘two.sided’ based on the alternative hypothesis.

conf. level: confidence level of the interval

prop.test() :

If n >30 i.e when sample size is large then we use prop.test() function to perform one -proportion z-test.

The prop.test() function uses the following basic syntax:

prop.test(x, n, p = NULL,
          alternative = c("two.sided", "less", "greater"),
          conf.level = 0.95, correct = TRUE)

where:

x : The number of successes

n: The number of trials.

p: The vector of probabilities of success.

alternative: The alternative hypothesis for the test.It can be ‘greater’, ‘less’, ‘two.sided’ based on the alternative hypothesis.

conf. level: confidence level of the interval.

correct: a logical indicating whether Yates’ continuity correction should be applied or not where it is possible.

Summary for the one sample Proportion Z-test

	Left-tailed Test	Right-tailed Test	Two-tailed Test
Null Hypothesis	H0 : p≥p0	H0 : p≤p0	H0 : p=p0
Alternate Hypothesis	Ha : p<p0	Ha : p>p0	Ha : p ≠ p0
Test Statistic	z= (p^ – p0)/√(p0(1- p0 )/n	z= (p^ – p0)/√(p0(1- p0 )/n	z= (p^ – p0)/√(p0(1- p0 )/n
Decision Rule: p-value approach (where α is level of significance)	If p-value ≤α then Reject H0	If p-value ≤α then Reject H0	If p-value ≤α then Reject H0
Decision Rule: Critical-value approach	If z ≤ -zα then Reject H0	If z ≥ zα then Reject H0	If z ≤ -zα/2 or z ≥ zα/2 then Reject H0

How to do one proportion z-test in R?

We will calculate the test statistic by using one proportion z-test.

Procedure to perform One Proportion Z-Test in R

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

Step 2: Decide the level of significance α (alpha).

Step 3: Calculate the test statistic using the binom.test() or prop.test() depending upon the sample size.

Step 4: Interpret the one-proportion z-test results.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Let’s see practical examples that show how to use the binom.test() or prop.test() function in R.

Examples of One Proportion z-test in R

Example 1: Right-tailed one proportion test in R

An auditor for the Online Service wants to examine its special two-hour priority order delivery to determine the proportion of the orders that actually arrive within the promised two-hour period. A randomly selected sample of 1500 such orders is found to contain 1150 that were delivered on time. Does the sample data provide evidence to conclude that the percentage of on-time orders is more than 75%? Test at 5% level of significance.

Solution: Given data :

sample size (n) = 1500

number of success (x) = 1150

sample proportion (p^{^}) = x/n = 1150/1500 = 0.7666

hypothesized population proportion (p₀) = 0.75

level of significance (α) = 0.05

confidence level = 0.95

Let’s solve this example by the step-by-step procedure.

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

Let p₀ denote the hypothesized value for the proportion.

p denotes the population proportion

Null Hypothesis: The population proportion is equal to 0.75 (i.e. 75%).

H₀ : p= 0.75  (right-tailed test)

Alternate Hypothesis: The population proportion is greater than 0.75 (i.e. 75%).

H_a : p > 0.75

Step 2: level of significance (α) = 0.05

Step 3: Calculate the test statistic using the below code.

Since here sample size = 1500 >30.

So we use prop.test() in this example.

# Perform one-proportion z-test

prop.test(x=1150, n=1500, p=0.75, alternative="greater")

Specify the alternative hypothesis as “greater” because we are performing a right-tailed test. The results for the one-proportion z-test are as follows.

#Results
1-sample proportions test with	continuity correction

data:  1150 out of 1500, null probability 0.75
X-squared = 2.1342, df = 1, p-value = 0.07202
alternative hypothesis: true p is greater than 0.75
95 percent confidence interval:
 0.7478919 1.0000000
sample estimates:
        p 
0.7666667 

Step 4: Interpret the one-proportion test results.

How to interpret one proportion z-test results in R?

Let’s see the interpretation of one-proportion z-test results in R.

data: This gives information about the data used in the one-proportion z-test.

X-squared: the value of Pearson’s chi-squared test statistic.

df: the degree of freedom of the approximate chi-squared distribution of the test statistic.

p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.07202.

alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis is population proportion is greater than 0.75 i.e. right-tailed.

95 percent confidence interval: This gives us a 95% confidence interval for the true proportion. Here the 95% confidence interval is [0.7478919,1.0000000].

sample estimates: It gives the sample proportion. In our case, the sample proportion is 0.7666667.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Conclusion:

Since the p-value[ 0.07202 ] is greater than the level of significance (α) = 0.05, we fail to reject the null hypothesis.

This means we have sufficient evidence to say that the population proportion is equal to 0.75.

Example 2: Two-tailed one proportion test in R

In a sample of 20 students in College,11 are tea-drinkers and the rest are coffee-drinkers. Can we assume that both tea and coffee drinkers are equally popular in college at the 5% level of significance?

Solution: Given data :

sample size (n) = 20

Number of tea-drinkers (x)= 11

sample proportion (p^{^}) = number of tea-drinkers /sample size

p^{^} = 11/20 = 0.55

Let’s solve this example by the step-by-step procedure.

Step 1: Define the Null Hypothesis and Alternate Hypothesis.

let p be the population proportion for the tea drinkers.

Null Hypothesis: Both tea and coffee drinkers are equally popular in the college

H₀ : p = 0.5

Alternate Hypothesis: Tea and Coffee drinkers are not equal in college.

H_a : p ≠ 0.5

Step 2: level of significance (α) = 0.05

Step 3: Calculate the test statistic using the below code.

Since here, sample size = 20 <30.

So we use binom.test() in this example.

# Perform one-proportion z-test

binom.test(x=11,n=20,p=0.5,alternative = "two.sided")

Specify the alternative hypothesis as “two.sided” because we are performing a two-tailed test. The results for the one-proportion z-test are as follows.

#Results
Exact binomial test

data:  11 and 20
number of successes = 11, number of
trials = 20, p-value = 0.8238
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.3152781 0.7694221
sample estimates:
probability of success 
                  0.55 

Step 4: Interpret the one-proportion test results.

How to interpret one proportion z-test results in R?

Let’s see the interpretation of one-proportion z-test results in R.

data: This gives information about the data used in the one-proportion z-test. It tells the number of successes and the number of trials.

p-value: This is the p-value corresponding to a statistic. In our case, the p-value is 0.8238.

alternative: It is the alternative hypothesis used for the z-test. In our case, an alternative hypothesis is a Tea and Coffee drinkers are not equal in college, i.e. two-tailed.

95 percent confidence interval: This gives us a 95% confidence interval for the true proportion. Here the 95% confidence interval is [0.3152781,0.7694221].

sample estimates: It gives the probability of success. In our case, the probability of success is 0.55.

Step 5: Determine the rejection criteria for the given confidence level and conclude the results whether the test statistic lies in the rejection region or non-rejection region.

Conclusion:

Since the p-value[0.8238] is greater than the level of significance (α) = 0.05, we fail to reject the null hypothesis.

This means we have sufficient evidence to say that tea and coffee drinkers are equally popular in college.

Summary

I hope you found the above article on One Proportion z-test in R with Examples informative and educational.